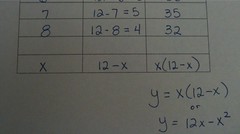The move to middle school has really allowed me to consider not only why we do what we do, but why students do what they do. I had one such opportunity the other day during my introduction to quadratics.
I gave my students the "magic number" worksheet where they choose a number and then select integer pairs whose sum is the magic number and place them in a table. The third column of the table is the product of the integers.
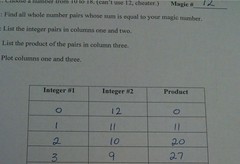
Filling out the table took all of 30 seconds because my students are very good at following directions.
Plotting the relationship between columns 1 & 3 went very smoothly as well. So smoothly that students were very nonchcalont about the symmetry of the resulting parabolas.
Things got interesting when I asked them to give me an equation that represented the relationship between column 1 and column 3. It was interesting to me when I asked them what was happening in column 2.
Most students saw column 2 through the lense of addition. For example, if the magic number was 12 and the number in column 1 was 4, students would mentally figure,
"4 + what = 12?"
The answer's 8. Obvious. And they got this answer as if it were a thoughtless reflex.
As long as column 1 contained an integer, there was no problem. However, this was no help when it came to generalizing an equation. As a result, many students struggled with going from the concrete to the abstract.
"What's happening in column 2?"
"Addition."
"Look again. Is it really addition?"
"No, subtraction. You're subtracting in column 2."
"OK, so what happens if we write column 2 like this...

...and then let column 1 be x?"
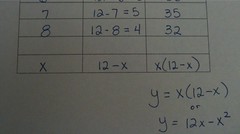
"Ooooh, column 2 is 12-x."
Recognizing what was happening in column 2 made finding the equation simple. The real problem was that there was a disconnect between what they thought they were doing and what they actually were doing.
This led to a nice discussion on what I like to call "taking thoughts captive." Teachers call it metacognition. Students call it...well, they don't call it anything, because they don't usually realize they're doing it.
Somewhere in there is the reason we get a shoulder shrug and an "I don't know" when we ask questions.
But once they realize that they ask themselves questions hundreds (maybe thousands) of times each day, it's impossible for them to not think about it.


 Yeah, gotta say I love this feature. Finding questions with good distractors is tough at best. But if you decide on an algorithm based on common misconceptions, you're good to go. In this problem, I decided the common misconceptions for students calculating slope based on a graph were:
Yeah, gotta say I love this feature. Finding questions with good distractors is tough at best. But if you decide on an algorithm based on common misconceptions, you're good to go. In this problem, I decided the common misconceptions for students calculating slope based on a graph were: